
It is fair to argue that in the short history of game studies, the concept of graphical projection has not been used in all its dimensions. In a way, we might even say that the idea has been systematically overlooked. Therefore, in order to fully express the potential of graphical projection in game studies, we have to properly define the vocabulary used to describe its various forms. Indeed, while the press and gamers have only applied catch-all terms like top-down view and isometric graphics, researchers need a more robust and complex categorization of each type of projection. My opinion is that a proper use of the language of visual arts will provide a more robust analytical tool for game studies.
The main idea is to use terms in keeping with the traditional perspectives from which they derive. Certainly, I don’t want to apply (as a copy-paste) the terms only because they fit into a type of effect of one technology or another, but instead we need to understand the principles of each type of projection and find its own application as a video gaming figure of speech. To accomplish this, we have to recognize the historical aspect of the concept of graphical projection and its relation with today’s digital imaging.
Out of which tradition—mathematical, scientific or artistic—should we envision graphical projection? As we search through art history for a precise definition, we face a historical and conceptual dead end. Perspective, for instance, has always been torn between its more practical aspects and its more scientific conceptualization. Graphical projection, as a practical concept, answers a defined objective: make visually intelligible a three dimension view on a flat surface. As such, graphical projection is a protocol in which every form has its own rules.
If we take, for example, the principle of Albertian perspective, the fundamental idea was more concerned with creating a working tool to coordinate the space of the frame than an artistic or philosophical concept. Alberti was, above all, a mathematician. Thus, his theory on perspective was predominantly influenced by the optical principles of Euclid. That cold and scientific conception of the principle of vision has had a major impact on Alberti’s logic of representation—which, according to Damisch (1987), still dominates certain principles of the current logic of visual representation such as the predetermined viewpoint of the artist and the viewer.
Indeed, Albertian perspective is a mathematical construct as the perception combines the perfect vantage point (of the artist and the viewer) and the vanishing point (where all lines converge). This point, the founding point, is the most important because it guides the viewer (it tells them where to look) and directs all the other points of the picture. Finally, because it only offers a single viewing position, it encodes the visual representation. The visual experience related to this ‘mathematical’ perspective of Alberti is a spatial relationship dictated by the artist, and not drawn from the real laws of physics or the principle of photographic representation. This distinction is important to our current relationship with visual arts which is the mathematization of visual representation by digital technology.
According to Friedberg (2006), the surface of today’s screen (computer or television) is divided into several components and functions that we analyze simultaneously, a bit like a cubist painting. Indeed, this particular type of painting, unlike the works of Italian Renaissance using Albertian perspective, simultaneously offers a multitude of views. Also, and perhaps most importantly, cubist painting has fractured the single viewpoint of Albertian perspective and placed disparate objects on the same representational plane. This paradigm of Albertian perspective is nonetheless ingrained in video games and any other situation that requires the simulation of three dimensional space. The visual simulation in video games and its objective (to provide a virtual playground rather than an optimization of a visual space) makes it closer to Italian Renaissance art history than modern art. In this case, our standpoint on perspective is the same as Damisch: it is a paradigm that can pass through and amalgamate history.
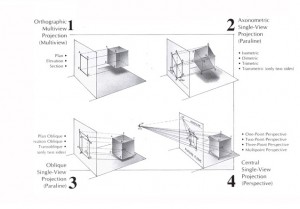
Graphic projection systems
The two types of projection in a nutshell
As we discussed a little earlier, perspective has been the principal technique for artists to model their perception. Also, we saw how this form of projection is combined with the idea that visual representation is predetermined as a mise-en-scène by the artist (and thus, not by nature). As such, perspective is a great tool for painters to draw attention on a specific element of the representation and not only give an impression of a third dimension. However, there is another form of projection—called parallel projection—that tries to illustrate a third dimension on a flat surface, and one has to know how to differentiate them.
Even though perspective and parallel projections have a similar main objective, as techniques, they are quite different. In parallel projection, lines that are parallel in reality are drawn parallel in the picture; contrary to perspective, there is no foreshortening involved to approximate the vision that an actual human being would have. The main focus in this kind of projection is on the axes between the lines. As we saw, perspective is more about representing the viewpoint than the object it represents. To summarize, perspective projection is using the process of convergence of parallel lines toward one (or more) vanishing point(s) and implies a horizon line. Parallel projection uses the method of projecting straight lines. Therefore, both parallel and perspective projections have their own specific categories with their own specifications.
A guide to parallel and perspective projection
Parallel projection is divided into two categories: pictorial projection and orthographic projection. Orthographic projection is a process derived from the principles of descriptive geometry. However, since it is mainly used in the execution of technical and working drawing, this category will not be used to follow the objective of our study. Pictorial projection tries to represent an object as viewed in an angle so that all three directions (axes) of space will be visible in a single picture. In order to do so, pictorial projections contain some distortion and liberties in the representation of the object.
In pictorial projection, the projected image is drawn according to the parallel lines that make up the grid of represented space, which means that the parallel lines of an object in reality remain parallel in the drawn image. Pictorial projection is divided into two categories: axonometric and oblique projections. What distinguishes the oblique and axonometric projection is their relationship to the projective plane. The projective plane is an extension of the mathematical concept of plane in which two parallel lines can eventually meet at infinity. In other words, the projective plane can be imagined as a two dimensional space where one can project a third dimension using infinite projection points.
Oblique projection is the simplest representation of parallel projection. In oblique projection, one face of the projected object is presented parallel to the projective plane and the lines are drawn at an angle other than 90 degrees. The cavalier perspective and the cabinet projection are the forms most commonly used in oblique projection. The cavalier perspective, despite its name, is not a form of perspective, but a pictorial projection, since the lines that are projected are based on a specific angle and not a vanishing point. The method is more mathematical than artistic: the coordinates of the points x and z of the image are reported in a ratio of 1:1 and the point y is drawn at a specific angle (generally 30 or 45 degrees). The principle is the same for cabinet projection, however, the point y will be drawn in a ratio of 0.5 of its length. Oblique projection is mostly used in technical drawings and illustrations. However, before the advent of 3D, some video games have used this form of projection in the visual aesthetics of their design, such as Paperboy, Sim City and Ultima VII.
Axonometric projection is the method of parallel projection in which the axes of the object represented are not parallel to the projective plane in order to represent all three points of views (x, y and z). Depending on the division of the sum of all three angles forming the axis of the projected object, axonometric projection uses three more specific terms: isometric, dimetric and trimetric projections. Because it is the most common form of axonometric projection, isometric has often taken the role (and the name) of a vast number of other categories of visual representation. However, isometric, as a technique of representation, has its own specific set of rules and visual effects. Indeed, the angles of an isometric projection are always of 30 degrees. The same scale is used on all axes, which meets the actual proportion of the object in all three dimensions. Dimetric projection highlights two of the three axes by making their angles equal. There are therefore two different scales: a scale which is the same for two axes (for example, the axis x and z for width and depth; and a second one to regulate the third axis, the y axis, i.e. the height). Trimetric projection shows the three axes with different values and therefore three different scales, one for each axis. To clarify our point, we could give the examples of Final Fantasy Tactics to illustrate isometric projection, Diablo for dimetric projection, and Fallout for trimetric projection.
As we have seen previously, perspective and parallel projections both have the same main objective: to render a tridimensional view on a flat piece of paper. Indeed, perspective uses its own techniques of illusion to represent as closely as possible the direct view of the artist’s eye. These techniques are mainly based on the illusion of depth, and the various techniques include the effect that distant objects are smaller than closer ones. Also, perspective projection implies greater subjectivity and adaptation on account of the artist. It is therefore less mathematical or geometric than parallel perspective, which is based on the degree of the angles between the projected lines. In this sense, perspective projection has two tangents: fundamental and artificial. The fundamental perspective is more based on the use of color to give a sense of depth. For example, chromatic perspective uses the relational effects between colors to achieve depth by using warm foreground colors and cold background colors. Artificial perspective is rather a construction of the pictorial space (like Albertian perspective).
Before the invention of artificial perspective, the coherence of the picture space was established by the existing pictorial conventions (Greek or Egyptian for instance), or by intuition, and was therefore fundamental. From ancient Egypt to ancient Greece, different techniques and various depth cues were used to simulate a third dimension without any mathematical calculations: overlapping objects, a multitude of planes, a color gradient, shadow and light, the checkerboard floor so often seen in Dutch paintings of the 17th century such as those of Vermeer and de Hooch, etc. Some of these techniques are still used today to reinforce the simulation of a third dimension in addition to another form of projection in videogames as well as in painting. Artificial perspective dates back to the Renaissance, and is rooted in a mathematical (Ptolemy, Euclid), optical (Alhazen), geometric (Brunelleschi) and physical (Aristotle) basis. Its study was particularly established by the theoretical works of Alberti in De Pictura (1435).
Perspective mainly uses the process of convergence of parallel lines toward one or more vanishing points and an implied horizon line that often serves to support those vanishing points. With one vanishing point, the main focus is usually located in front of the viewer and the horizon, at the center of the picture (which recalls railway tracks). Perspective with two vanishing points is typically used to illustrate a pair of parallels (obliques) that converge within the image and away from their respective vanishing points. One can add a third vanishing point to the perspective, usually located either well below or well above the element represented. The three vanishing point perspective is regularly used in technical drawing, but not as much in video gaming.
As we have discussed, perspective and parallel projections do not proceed in the same way to achieve the illusion of three dimensions nor do they have the same visual relation with the object they try to illustrate. While perspective is subject centered and tries to simulate human vision, parallel projection is object centered and tries to simulate the actual physical dimensions of an object independently of any actual view we would have of it. As such, perspective projection, unlike parallel projection, is closer to the concept of human vision (or at least its Euclidean concept). This means that the underlying principle of perspective is the focus on a point (the vanishing point), and all the lines are projecting toward this point. Being closer to the concept of human vision also means appealing to the principle of foreshortening. This principle is recognized by the impression of compression and distortion of the object it represents, related to the perspective since the object is facing the viewer. It was used particularly in the Middle Ages, but we can easily recognize its combination with some technological techniques in video games graphics (like Mode 7 in F-Zero).
With the advent of the moving image, other depth effects were matched to projection techniques. First, there is the parallax effect, which corresponds to the way objects move laterally at different speeds depending on the distance which separates them from the viewer. We can easily distinguish the effect by its principle of visual motion: the closer the objects represented in the image are to the viewer, the faster they move. There is also the stereoscopic effect that gives the illusion of depth. To achieve this visual effect, we need two similar images (but with a slight shift) and a technical device that merges these images into one. The stereoscopic effect has been widely researched and used, and should be, if we believe the discourse of advertising papers, the ultimate indicator of technological advance in games, consoles, and among other visual projection industries. However, the success of a console using the principles of stereoscopy have been limited, as evidenced by the recent Nintendo 3DS.
Visual projection in video games
As mentioned above, some terms are used more often than others in video game discourse, and this is not just a question of referential accuracy or mere habit, but rather simple resumption semantics. However, now the structure of the different techniques of graphic projection have been developed, it would be appropriate to use the proper semantic terms.

Friday The 13th
Video game graphics can be presented sideways (side view), from the top (top-down view) or from a straight down view (bird’s eye). The side view is often used to simulate the “eye of the beholder”. These types of projection are often used in 2D games. Sometimes they deviate slightly from projection rules in order to “add variety and the illusion of depth without the use of scaling” (Koncewicz, 2009) which is a calculation process of shrinking or growing 2D graphics objects (sprites). One of the most famous examples of side view gaming is Super Mario Bros. This game is interesting in terms of how it demonstrates that the side view projection is appropriate, thus without using any technique to illustrate depth. Indeed, those types of presentation are not exclusive to parallel or perspective projection. Also, this type of viewpoint frequently uses the parallax effect, which, as mentioned earlier, provides a sense of depth. Good examples of side scrolling games using parallel projection are Donkey Kong Country 2 and Prince of Persia. Some video games using perspective projection are also presented sideways, such as Friday the 13th. However, in this videogame, although everything seems to be in two-dimension (like the houses, or the background), there are projected lines that make the interpretation of the depth strange and vague. It is in an effort to create depth in that the two oblique lines in front each house or road implies a distance. But still, because these lines do not correspond to each other to a single vanishing point, it offers a rather odd presentation. Which means that side-scrolling is not infallible to coherence in graphical projection.

The Legend of Zelda
The principal problem with other points of view (top-down and bird’s eye) and the types of projection is that the angles tend to be confused with one another. We can often see different types of projections in the same frame, which gives a strange perception of the objects or the view represented. For example, in the interior representation in The Legend of Zelda, the top-down view offers a simultaneous impression that the player’s view is from above and frontal. Indeed, there is a strong one point perspective with a central vanishing point to the character which we see frontally thus the gameplay suggests a side-scrolling motion (which, in that case, the character is moving while laying down). Despite this, this point of view was frequently used in certain types of games because the overhead view often offers the best viewpoint for gameplay. This is particularly the case for role playing games (Final Fantasy, Dragon Warrior, etc.), strategy games (Warcraft), or construction and management simulation games (RollerCoaster Tycoon, SimCity 2000, etc.).
As stated before, in parallel projection the relationship between the axes is preferred to the impression of horizon or depth. In an isometric view, the scale of all three dimensions (x, y, z) is the same, and each angle measure 30 degrees. A cube projected isometrically retains its proportions, which means that its width, height and length will be the same size and will contain the same surface area. This type of projection is in fact very difficult to achieve (especially in the older games), and designers prefer to use a dimetric projection. The main difference between an isometric and a dimetric projection is that in the latter, only two out of three angles must respect the equivalence of the axes. For this reason, this type of projection is the most generally used. The most common ratio of angles is 2:1 (for every two pixels on the x axis, there is one on the y axis). This means that most of the time, an isometric projection is actually dimetric because this combination of pixels does not result in a 30 degree angle. Finally, trimetric projection allows freedom to stylize angles, and therefore graphics, which can result in an atypical game stylization. Since oblique projection has no specific rules concerning the angles of the axes, its aesthetic results in a quite arbitrary scaling of dimensions and proportions. However, as mentioned before, the cavalier perspective and cabinet projection (based on an extension of the sides of an object at an angle of 30 or 45 degree) was used in some games (such as the original Sim City).
As suggested at the beginning of this article, with regard to the historical study of graphics in video games, perspective is much more relevant than parallel projection because it is a paradigm that fits better with new technologies within time. Yet, according to Friedberg, the advent of new technologies has broken the single view point of this traditional visual conception. This challenge towards perspective by new technologies is perceived by the recent and rapid reorganization of the layout of images on modern displays. The split screen and multiple screens are two examples of resistance to the dominant visual mode dictated by the paradigm of perspective (single frame/single image). Although certain technologies have changed our relationship to the screen and the way we perceive our visual space, I believe that video games are rather a simulation than an exploration or organization of the screen. Indeed, even though the screen may be divided or include disparate elements in its visual space (such as commands, tools or actions), the main objective of the game will focus on a function of simulation rather than an organization one (like in the case of a cell phone or desktop display). Perspective is therefore an effective and appropriate tool to explore the advent of three dimensionality.
Perspective in 2D games was mainly used to complement the background of the first adventure games. Perspective to a vanishing point facilitated the calculation of the scaling (characters, for example). The environments made of pre-rendered 3D graphics allow the player to occupy any point of view in the environment and the characters therein were resized accordingly. This way the depth was integrated into the gameplay [endnote See the paper in this issue by Dominic Arsenault and Pierre-Marc Côté, Reverse-Engineering Perspective Innovation: An Introduction to Graphical Regimes.]. However, the use of perspective in games in 2D and fixed 3D was not the norm until the advent of real time 3D. The use of perspective was mostly devoted to decorative elements or to the environment.
Games like Prince of Persia and Mortal Kombat may not have been in actual 3D, but they advanced graphics technologies for video games. The digitized actors that portrayed the in game characters in Mortal Kombat, for example, were developed from digitized sprites of real actors, not animated cartoons. However, the multiplicity of characters is not from an equal number of actors, but from the recoloration of sprites. Indeed, some of the characters were based on the same model, but the colors of their attire and their special techniques indicated that they were different (such as Scorpion, Reptile and Sub-Zero). In 1997, Mortal Kombat 4 led the franchise to three dimensionality by replacing photographic actor models with polygon models from motion capture, thus moving from fixed 3D to real life 3D (Elmer-Dewitt, 2001).
Since the advent of polygonal 3D, the use of perspective is almost systematic. However, it is not the fact of having a good graphic rendering or appropriate use of perspective that makes a game a success or a failure of. Although all games use their own projection technique, one has to keep in mind that it is a specification among many others in the theory of video games. Thus the reception, the gameplay, and many other factors still remain to be studied. In this perspective, the vocabulary of graphic projection is not to be taken literally, but should be applied according to the knowledge that game studies has its own history.
– All images belong to their rightful owner. Academic intentions only.-
References
Bordwell, D., & Thompson, K. (2010). Film History: An Introduction. New York, NY: McGraw-Hill.
Damisch, H. (1987). L’origine de la perspective. Paris, France: Flammarion.
Elmer-Dewitt, P. (2001, June 24). The Amazing Video Game Boom. Time magazine. Retrieved from http://www.time.com/time/magazine/article/0,9171,162405,00.html
Friedberg, A. (2006). The Virtual Window: From Alberti to Microsoft. Cambridge, MA: MIT Press.
Gombrich, E. H. (1977). Art and Illusion: A Study in the Psychology of Pictorial Representation. London, UK: Phaidon.
Koncewicz, R. (2009). A Layman’s Guide to Projection in Videogames. Significant bits. Retrieved from http://www.significant-bits.com/a-laymans-guide-to-projection-in-videogames
Nitsche, M. (2008). Video Game Spaces: Image, Play and Structure in 3D Worlds. Cambridge, MA: MIT Press.
Wiersma, O. B. (2008). Perspective Seen from Different Points of View. Retrieved from http://www.ottobwiersma.nl
Ludography
Diablo, Blizzard North, USA, 1996.
Donkey Kong Country 2: Diddy’s Kong Quest, Rare, UK, 1995.
Dragon Warrior, Chunsoft, Japan, 1986.
Fallout, Interplay Entertainment, USA, 1997.
Final Fantasy, H. Sakaguchi, Square, Japan, 1987.
Final Fantasy Tactics, Square, Japan, 1997.
F-Zero, Nintendo EAD, Japan, 1990.
Friday the 13th, Domark, UK, 1985.
Paperboy, Atari Games, USA, 1984.
Prince of Persia, Brøderbund, USA, 1989.
RollerCoaster Tycoon, C. Sawyer, Microprose, USA, 1999.
Sim City, W. Wright, Maxis, 1989.
SimCity 2000, W. Wright, Maxis, 1994.
Super Mario Bros, S. Miyamoto, T. Tezuka, Nintendo, Japan, 1995.
The Legend of Zelda, S. Miyamoto, Nintendo EAD, Japan, 1986.
Ultima VII: The Black Gate, R. Garriott, Origin System, USA, 1992.
Warcraft, Blizzard Entertainment, USA, 1994.
-Tutte le immagini appartengono ai rispettivi proprietari e sono usate ai soli fini accademici. –

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
