
Game developers, even during the early years of game design, have always searched for new and interesting ways of creating more elaborate, immersive and realistic environments for their video games.
Even the MUD’s (multi-user dungeons), designed in the late 1970s, such as Roy Trubshaw’s MUD1, implemented such interesting ways of connecting their rooms as teleportation, paving the way for later developers to design and implement interesting and imaginative environments that border on the fantastic or the Hyper-real, as we will designate these worlds in this article.
The term Hyper-real is used extensively by philosophers, such as Jean Baudrillard and Umberto Eco; they use the term to distinguish reality from a simulation of reality, especially in cases of technologically advanced societies. In Baudrillard’s own words, hyper-reality is a simulation generated “by models of a real without origin or reality” (Baudrillard, 2000, p. 1). In this article, the term “Hyper-real worlds” will be used to describe worlds that are not that much further from what Baudrillard describes. These game worlds, although they have a connection to our reality, architectural structure or geographical coordinates, are definitely un-realistic and without any origin in our world, comprised of fantastic creatures, alien architecture and geometrical and physical impossibilities.
This brings us to the second major topic of discussion for this article: impossible shapes. At this point, we must distinguish between two major categories of impossibilities in video game world design, geometrical/mathematical impossibilities and physical/temporal impossibilities. Even though in the mathematical and physical world, that we live in, space and time co-exist and are interdependent on one another, we have to separate them for the sake of better understanding what is possible and what is not when developing a video game. This separation is dictated by the simple fact that the computer hardware used to design, create and implement these virtual worlds is based on mathematical reasoning and not a physical one. While we will explore, to some extent, the geometrical/mathematical impossibilities in this article, best exemplified by the works of M.C. Escher, Oscar Reutersvärd, Salvador Dalí and Giorgio De Chirico among others, some notes on physical/temporal impossibilities will be given to showcase the possibilities that a developer is offered in order to create a hyper-real virtual world.
Besides exploring how impossible elements can be introduced in 2D, 2.5D and3D game worlds, it is necessary to gain basic knowledge of how the human visual system works in order to better understand the limitations imposed in the design process of game worlds that utilize stereoscopic imagery.
Concluding this article, we will assess what possibilities stereoscopic video games have to offer to potential game developers and the gaming audience and what opportunities these game worlds open up for future technologies that involve video game development.
The Art of the Impossible
Oscar Reutersvärd (1915-2002) is considered to be the father of impossible figures and shapes. During his long career as an artist he created thousands of impossible figures that seemingly break the laws of geometry and space. His most famous shape is the impossible triangle which later became more commonly known as The Penrose Triangle.
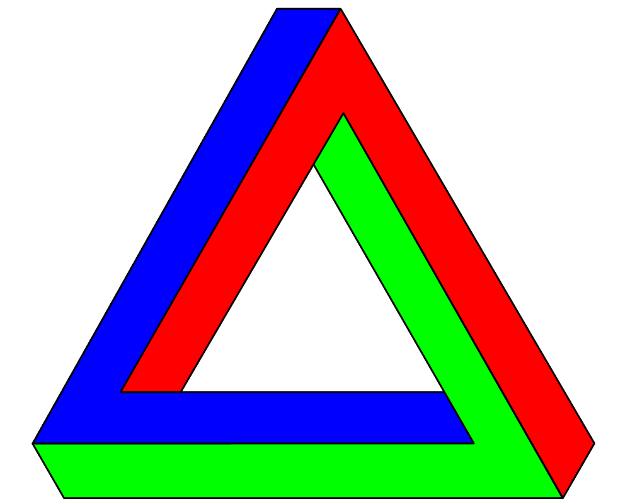
Fig. 1 the Penrose Triangle
M.C. Escher (1898 – 1972) is the major follower of Reutersvärd’s artistic perspective. While Reutersvärd dabbled only in designing shapes and objects that transcend the geometrical laws, Escher managed to incorporate these designs into his paintings, creating art–in the process–that transcend the Euclidean laws and also provided the inspiration for later artists and mathematicians–like Roger Penrose and Douglas Hofstadter–to try their own hand in creating impossible figures.
Two painters that could fit into the category of impossible artists are surrealist painters Salvador Dalí (1904-1989) and Giorgio De Chirico (1888-1978). Dalí, as a man with an excessive number of eccentricities, painted the world around him as only a man who claims to remember his birth could. Filled with, mostly, physical and biological impossibilities, his paintings prove to be a challenge for game developers who wish to emulate a world that resembles Dalí’s soft physics.
Where Dalí chose to paint physical and biological impossibilities, De Chirico’s paintings, on the other hand, though they seemed to be more accurate in the depiction of the real world, have nevertheless their own impossible touch. De Chirico chose to paint his own distorted versions of the world around him in the skewed perspectives offered by different fugue points in the same scene, using flawed perspective to prioritize order of perception.
The Human Perception
Visual perception is, perhaps, the most important sense of a human when locomotion and orientation are concerned, since it is not only the sense which enables us to visualize and interpret the world around us but also gives us the largest amount of information to do so. There are some instances when sound and the auditory perception take precedence over the visual system, especially where balance is involved, but the sheer amount of information entered through the visual system makes it the paramount sense when video games are concerned.
Everything about human perception starts with the upright position of the body which enables us to differentiate between front-back and left-right (Tuan, 2001).These positions are extrapolated from the position of the body and they change according to the body’s motion in space. The only axes that are relatively static are the top-bottom axes which would only change in case the body finds itself floating in a zero-gravity environment.
Furthermore, depending on the distance from the observer to the object observed, the distance can be differentiated into 3 categories: close-range (up to 5m from object), intermediate range (between 5m and 20m) and long-range (more than 20m) (Granum and Musaeus in Qvortrup et al., 2002, pp. 118-119).
The third most important factor in human perception is the search for landmarks and/or points of interest. According to Tuan (2001), a human cannot look at a scene in general since our eyes will always look for a place or scene to rest upon. Kevin Lynch also individuated landmarks as a defining element to create memorable spaces. This is done consciously (when we deliberately search for a landmark) or unconsciously (when a feature in the horizon is so compelling that it demands our attention).
There are, of course, many more factors that play a role, either major or minor, in the human perception system. Colors, size of objects observed, shapes, perspective, and object motion are only some of them, and even these factors can all be sub-divided into more elaborate and detailed sub-categories.
The Functions of the Eyes
Anatomically, the part of the brain that controls and is concerned with the reception and interpretation of vision is the visual cortex. This is a very curious function for two reasons.
Firstly, a region that exists on the far back of the brain is responsible for interpreting the visual signals that come from the front of the human head.
Second is the fact that the right cerebral hemisphere of the brain is responsible for the left-hand side of the body, and the left cerebral hemisphere is responsible for the right-hand side. That way, a well-defined map of the left-hand visual field is formed on the right visual cortex and another map is formed of the right-hand visual system on the left visual cortex (Penrose, 2002, pp. 484-485).
Aside from these anatomical details, there are two distinguished features of the eyes that play a prominent role to the way we see and perceive the world around us.
One of these details is that the eye is not the sole organ for perceiving the world around us but only a part of a system that consists of the moving eye, the moving head, the brain and the moving body.
With the above system in mind, we can divide the above into three separate visions: aperture vision, ambient vision and ambulatory vision (Kolstrup in Qvortrup et al., 2002, p. 243).
The above system is utilized and most prominent in FPS (first-person shooter) games such as Counterstrike, where quick avatar (body and head) movements and quick eye movement is necessary in order to rise above other players and survive in this fast-paced PvP (player versus payer) video game.
The second feature, the anisotropy of left and right, is mostly overlooked and people are generally only unconsciously aware of it.
Heinrich Wölfflin, an art historian, pointed out that paintings lose their meaning when they are turned into their mirror images. This happens, he realized, because images are read by the brain from left to right which, in turn, changes the way they are interpreted when inverted (Arnheim, 2004).Notably, even thoughthis is true for cultures with a left-right scansion of written text, it is not universally true for all humans, but mostly for humans in western cultures. Whether this distinction is biological or cultural is not in the scope of this article to analyse.
Mercedes Gaffron, a psychologist, investigated the phenomenon of the left and right anisotropy in the brain further, and related it to the dominance of the left cerebral cortex, which contains the higher brain functions of speech, writing and reading.
This function has been used extensively in video games to a greater or lesser extent. In almost all video games where the avatar of the player is required to stay alive in order to continue playing the game, the most important aspect of the UI (user interface), arbitrarily the health and possibly the resources of the avatar, are almost always placed on the top left of the screen. Consequently, the rest of the UI is placed in key areas depending on their significance to the player and the game mechanics.
Even in notable exceptions to this pattern we see the dominance of the left-side. In Dead Space the entire UI was integrated on the avatar of the player but even in that case we can distinguish the definite dominance of the left side in the way the camera is placed above the right shoulder of the avatar and in the fact that the health of the avatar is placed on his back which, due to camera placement, is on the left side of our visual field.
The Virtual World of 2 Dimensions
In the early days of video game design, developers had only a limited amount of tools to work with. The limitations posed by these tools and the hardware that was called to process the final product allowed for only a minor number of shapes to be developed as part of the video game’s assets.
Despite this fact, the early MUDs (multi-user dungeons), which were actually text-based video games, represented the first interactive virtual worlds that demonstrated and utilized impossible non-Euclidean spaces in their game world. Lacking a visual representation of the in-game virtual world, they nevertheless paved the way for hyper-real, impossible worlds.
Once the technology was developed so as to include a series of moving images in order to demonstrate the virtual world to the player, hyper-real worlds started becoming more and more elaborate in their representation. The most prominent examples of hyper-real and impossible/non-Euclidean worlds are Pac-Man and Asteroids. Interestingly, both games featured the exact same non-Euclidean feature, which was also the one offered in the early MUDs of the ‘70s. This feature enabled the player-controlled avatar (in whatever form) to transcend the space of the designed area of play by exiting from one side of the map and re-appearing on the other side, following only either a designated exit-entrance portal (in the case of Pac-Man) or adhering to the momentum of the avatar’s movement at the point of exit (in the case of Asteroids).
The same teleportation effect was later used in games, such as Eye of The Beholder II: The Legend of Darkmoon, in order to create impossible corridors which were also meant as a puzzle for the player to solve, if they wanted to continue on their quest in the game.
Two-dimensional video games were, in fact, ideal for representing and portraying impossible shapes and non-Euclidean environments. Leaving aside text-based games, which left almost all visual representation of the virtual world to the imagination of the player, early video games that utilized moving image sequences to simulate character/avatar movement had the potential to create the most accurately depicted Escher-like environments.
The key factor that contributed to such a fact is the lack of freedom on the part of the player. Just like in an Escher painting, the player of a two-dimensional virtual world is limited in only a fixed viewpoint of the world: the one offered by the two-dimensional image that is demonstrated to them at any given time. They cannot move in a manner that would transcend this limitation any more than a viewer of an Escher painting can take one of the impossible objects that he designed on his hand and rotate it so as to see it from every possible angle.
Isometric Worlds: The lack of perspective
During the early 1980s, a new method of representing the virtual world came to being with the introduction of isometric or pseudo-3D environments. These games offered a view of the virtual world that had a very close, but not exact, resemblance to how humans perceive the world around them.
While the term isometric has been dominant in describing games that employ a fixed perspective, it is actually one of three axonometric projections used in video games and industrial design. The other two are diametric and trimetric.
The first game to utilize such a viewpoint was Zaxxon, after which many more followed, creating more elaborate and sophisticated worlds that proved to be extremely popular in either isometric or trimetric projections like Populous, Civilization II, Diablo and Fallout.
Even in recent years, there are still games that employ these axonometric projections in their viewpoint as the standard. The more recent examples are StarCraft and Diablo III which both employ a viewpoint that is similar to isometric view although, since it was created and developed in Blizzard’s proprietary 3D engine, there is also some hint of true perspective in the game world.
While isometric view provided a more detailed experience for the players, it still remained an artistic construct since humans never experience their surroundings in isometric view but in perspective. Even so, just like their two-dimensional counterparts, isometric video games provided the unique possibility to represent mathematical impossibilities, as depicted in Reutersvärd’s and Escher’s shapes and paintings. The lack of freedom, on the part of the user-controlled camera, was again the key factor that allowed for such designs to be accurately represented in the game world.
As we will explain later in this article, having a fixed perspective is the only actual way of depicting accurately and approximately the impossible shapes and scenes of Reutersvärd’s and Escher’s paintings.
The 3-dimensional World
With the advent of 3D software came the emergence of true 3D computer graphics in the video game world. The engines which have been designed by various companies as the main developing tools of current-date video games operate in the same way, and follow in the footsteps of the major 3D software in the market.
Both the 3D software and the various game engines operate on meshes, and utilize cameras and lights to give life to the scene.
A mesh is a collection of triangular (or quadrilateral in some cases) contiguous, non-overlapping faces joined together along their edges. A mesh will consist of three basic elements, called faces, edges and vertices. Modeling of these meshes occurs when we use a computer to implement the mathematical construction of an object, by defining points in a 3-dimensional array, which is based in the X, Y and Z axis of geometrical space or otherwise called, a Cartesian coordinates system. Essentially, a mesh is the visual representation of a mathematical theoretical object in a Cartesian coordinate system.
The most basic of these meshes are the Platonic solids, or as they are more commonly called, regular polyhedra. Only five of these meshes can exist in 3-dimensional space and in order of number of faces are: the tetrahedron, the hexahedron (cube), the octahedron, the dodecahedron and the icosahedron. These five are the only meshes in 3-dimensional space that satisfy the very strong restriction of looking exactly the same at every vertex (Banchoff, 1996, p. 91).
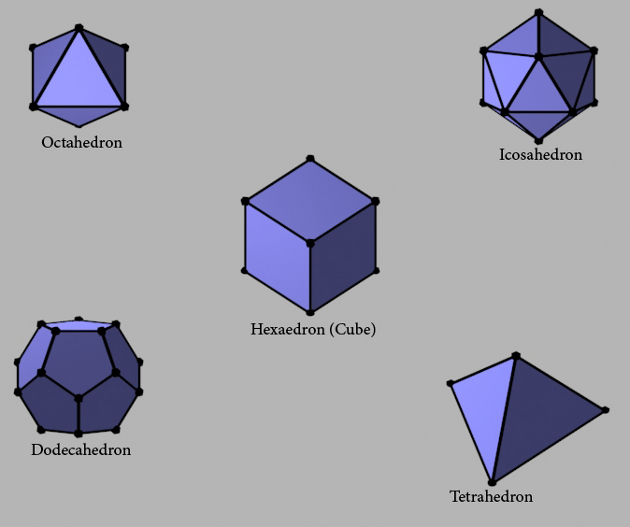
Fig. 2 Platonic Solids
Taking the cube as an example and imposing upon it the Cartesian coordinate system, we can see how it is interpreted, mathematically, in the 3-dimensional virtual world.
As we explained before, a mesh is modeled when the computer implements a mathematical construction of the object, by defining points in the Cartesian coordinates system. In the case of the cube, each vertex is defined that way, with a unique set of coordinates that each correspond to a unique location on the X, Y, and Z axes. Therefore, a cube can also be translated as a group of coordinate sets that have the form (X1, Y1, Z1), (X2, Y2, Z2)……(X8, Y8, Z8), with each set describing the exact position of every vertex of the cube in the Cartesian coordinate system.
Once we try to impose the same mathematical principles on the Penrose triangle, we immediately realize what the problem is. Since the Penrose triangle is a mesh, it is correctly identified as having faces, edges and vertices. The problem starts when we try to identify each vertex as a set of coordinates, corresponding to the 3 axes of the Cartesian coordinates system. What we discover is that each vertex of this object cannot be identified by only 3 specific points. Depending on the face (side) that this vertex belongs to, it will need at least 2 sets of coordinates for its mathematical construction, and in all the cases the coordinates of these sets will have at least one value that is not identical with each other. An example is shown in Figure 3 where we see that point x can be interpreted in two different ways, resulting in two different sets of coordinates for the (seemingly) same vertex depending on the viewpoint of the viewer. This means that in order for a Penrose triangle, or any other impossible shape for that matter, to be properly mathematically constructed in a virtual world, it must be done so in a 4-dimensional coordinates system or higher, depending on the object in question. Assuming that such a coordinates system existed, then any impossible object could be translated in the form of (X1, Y1, Z1, V1), (X2, Y2, Z2, V2)……(Xn, Yn, Zn, Vn), with each coordinate corresponding to a specific and unique position in the coordinates system.
The problem then is that a 4-dimensional (or higher) Cartesian coordinate system cannot exist in a 3-dimensional world. The reason for that is that 3D design software is based purely on mathematical and geometrical mechanics and the only way we can visualize objects with more than 3 dimensions is by using imagination and theoretical mathematics, as we will see below.
The best example of this limitation is the process used to create a Hypercube or Tesseract, a term attributed to C.H. Hinton who in the 1880’s wrote an article about the fourth dimension and his own dimensional allegory An Episode in Flatland (Banchoff, 1996, p. 115). This theoretical construct is supposed to depict a 4-dimensional cube in 3-dimensional space, virtual or real.
The logic behind creating such a construct starts with a point in space that has 0 dimensions. If we drag the point along the X dimension, we end up with a line, the first shape with a single dimension. By drawing the line along the Y dimension, we end up with a rectangle, the first shape with 2 dimensions. Drawing the rectangle along the Z dimension, we end up with a cube, an object of 3 dimensions. If we wish to go further than that, the only thing that we can do is drawing each vertex of the cube outwards, thus creating a cube inside a cube. But the truth is that this construct is nothing more than a 3-dimensional cube inside a 3-dimensional cube, not a 4-dimensional cube. A 4-dimensional cube, in a 4-dimensional Cartesian coordinate system, should have all its sides equal and all its angles right, and our construct has at least two sides which are not equal and at least two angles which are not right.
In an attempt to impose a new coordinate plane in the typical Cartesian coordinates system, we find that it is impossible to do so without deviating from the mathematical laws of the system. In three-dimensional space, a Cartesian coordinate system is defined by starting with three number lines intersecting at their common origin (0, 0, 0). On the first axis, the points are labeled as (x, 0, 0), on the second axis the points are labeled as (0, y, 0) and on the third axis the points are labeled as (0, 0, z). Thus, the points of a cube, designed in three-dimensional space, with a side length of 1 unit will be labeled:
| (0, 0, 0) | (0, 0, 1) |
| (1, 0, 0) | (1, 0, 1) |
| (1, 1, 0) | (1, 1, 1) |
| (0, 1, 0) | (0, 1, 1) |
(Banchoff, 1996, pp. 160-161)
Since algebra is practically the same whether we write theorems about one, two, three or four dimensions, we can extrapolate the same method to design a hyper-cube in a four-dimensional Cartesian coordinate system by working backwards.
A hyper-cube will consist of 16 points since it is created by dragging a cube towards a 4th dimension, essentially creating a second cube or a cube inside a cube. In a four-dimensional Cartesian coordinate system the points of a hyper-cube with a side length of 1 unit, will be labeled:
| (0, 0, 0, 0) | (1, 0, 0, 0) | (1, 1, 0, 0) | (0, 1, 0, 0) |
| (0, 0, 1, 0) | (1, 0, 1, 0) | (1, 1, 1, 0) | (0, 1, 1, 0) |
| (0, 0, 1, 1) | (1, 0, 1, 1) | (1, 1, 1, 1) | (0, 1, 1, 1) |
| (0, 0, 0, 1) | (1, 0, 0, 1) | (1, 1, 0,1) | (0, 1, 0, 1) |
(Banchoff, 1996, p. 162)
Following the information contained in the above table, we arrive at the conclusion that a four-dimensional Cartesian coordinate system should have four number lines intersecting at their common origin (0, 0, 0, 0). The first axis has points labeled as (x, 0, 0, 0), the second axis has points labeled as (0, y, 0, 0), the third axis has points labeled as (0, 0, z, 0), and the fourth axis has points labeled as (0, 0, 0, v). Any point within this Cartesian coordinate system is completely determined by the number quadruple (x, y, z, v). The problem is that any of the infinite lines that intersect the origin (0, 0, 0) of the three-dimensional Cartesian coordinate system, apart from x, y and z, is completely determined by the number triplet (x, y, z) which means that it will never obey the rule of the axis v which must have points labeled (0, 0, 0, v). Since this rule cannot be obeyed, and therefore, such a line cannot be created, a true fourth-dimensional Cartesian coordinate system can exist only in theory.
So, since it is impossible to create a 4-dimensional coordinates system, how can we, then, create impossible shapes, objects and scenes in a virtual world? The short answer, of course, is: we can’t. To find a solution we have to go back and explore the 2D and axonometric relatives of the current video games. There we find the solution for creating an impossible object or scene in a video game using current day technologies: keeping the object or scene in question fixated on a single angle towards the camera. Since all mathematical representations of impossible objects, on a Cartesian coordinate system, rely on being seen from a specific viewpoint, the same trick can be employed when trying to implement such an object into our 3D world. Keeping the object fixated on the correct angle towards the camera/player we keep the illusion of the object intact, for if the player could maneuver around the object, then he would recognize the truth of the object and the illusion would be lost.
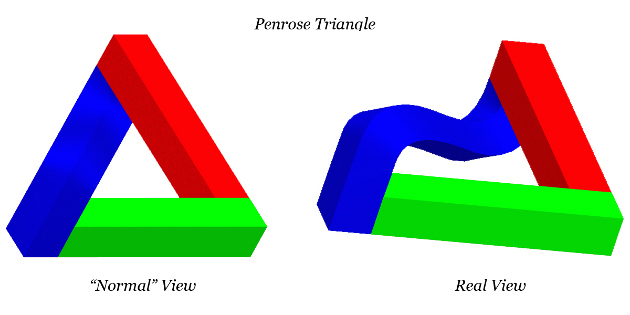
Fig. 3 – Tridimensional Penrose Triangle
In this way, we are free to manipulate these objects to any extent so as to make them appear exactly as they were designed by Escher and Reutersvärd.
Stereoscopy, the Road to Virtual Reality
Stereoscopic video games have already appeared back in 1982 with the game Sub-Roc 3D, an arcade game that used a display that delivered different individual images to the player’s eyes. Since then, many video game developers have created stereoscopic video games. Some of the most prominent titles in the video game industry are Duke Nukem 3D, Minecraft, Batman:Arkham City and, more recently, Assassin’s Creed III.
The basic requirement for stereoscopic 3D images is using two cameras to capture left and right eye images. These cameras are positioned in such a way so as to mimic the eye’s stereo vision capability by seeing two different angles of the same scene, with only a slight difference. The human brain then will take those two images and create a sense of depth (Shaw, 2011).
Despite the fact that stereoscopy gives a sense of depth and greatly enhances, in some cases, the 3D experience of the viewer/player, it still must obey and conform to the same rules outlined above concerning the design and implementation of 3D objects in a virtual environment.
Since stereoscopy needs two separate cameras to capture the same scene, impossible objects such as the Penrose Triangle will be even more difficult to depict, due to the fact that even if one of the cameras deviates even a little from the ‘normal’ viewpoint, that allows the object to be seen as impossible, and the illusion of the object is lost.
While stereoscopy is a technique that could provide excellent results for future video games, it will still be unable to represent impossible objects and scenes in a virtual environment.
Even in systems such as the Cave Automatic Virtual Environment (CAVE), which creates the illusion of a seamless virtual space by using projected stereoscopic images from the rear of the interactor, the illusion of an impossible object will be lost should the interactor in the CAVE box be moved to the side or behind, or the viewpoint deviated slightly from the ‘normal’ viewpoint (Nitsche, 2008, p. 211).
Just as axonometry paved the way for current era 3-dimensional environments in video games, by the same token, stereoscopy will pave the way for future virtual reality environments. But even then, impossible objects will still remain impossible, adhering to the absolute rules of geometry and mathematics since, after all, Virtual Space is a world defined by a universe of coordinates (Nitsche, 2008, p. 191).
Conclusions
Over the course of this article, we explored the world of 2D, axonometric, 3D and stereoscopic 3D video games in order to better understand the virtual world in which they exist.
As stated in the introduction of this article, separating the dimensions into geometrical, temporal and physical ones was paramount in order to discuss the possibilities offered in a world that is governed by mathematics, geometry and Cartesian coordinates, rather than biological or physical phenomena.
After examining the possibilities offered by current day technologies and their by-products, it is then safe to assume that impossible objects will not be able to exist in a virtual environment, exactly as they are unable to exist in our real 3-dimensional world.
Four hundred years ago Galileo Galilei, using his telescope, saw moons orbiting Jupiter and now, with modern day telescopes scientists can see and observe the presence of Quasars and distant solar systems that exist billions of light years away. The capacity of mankind to exceed its limitations might, one day, revolutionize our ability to realize the wonderful scenes and objects depicted by Escher’s paintings or Reutersvärd’s “Windows in the Floor.”
References
Arnheim, R. (2004). Art & Visual Perception: A Psychology of the Creative Eye. Berkeley, CA: University of California Press.
Banchoff, T.F. (1996). Beyond the Third Dimension: Geometry, Computer Graphics and Higher Dimensions. New York, NY: W.H. Freeman & Company.
Baudrillard, J. (2000). Simulacra and Simulation. Ann Arbor, MI: University of Michigan Press.
Lynch, K. (1960). The Image of the City. Cambridge, MA: MIT Press.
Nitsche, M. (2008). Video Game Spaces: Image, Play and Structure in 3D Worlds. Cambridge, MA: MIT Press.
Penrose, R. (2002). The Emperor’s New Mind. New York, NY: Oxford University Press.
Qvortrup, L. (Ed.). (2002). Virtual Space: Spatiality in Virtual Inhabited 3D Worlds. London, Great Britain: Springer-
Shaw, S. (2011, August). The Basics of Shooting Stereoscopic 3D – Part 1. 3droundabout. Retrieved from http://3droundabout.com/.
Tuan, Y.F. (2001). Space and Place: The Perspective of Experience. Minneapolis MN: University of Minnesota Press.
Video Games
Assassins Creed III, Ubisoft Montreal, Canada, 2012
Asteroids, Atari Inc., USA, 1979
Batman: Arkham City, Rocksteady Studios, UK, 2011
Civilization II, MicroProse, USA, 1996
Counterstrike, Valve Corporation, USA, 1999
Dead Space, EA Redwood Shores, USA, 2008
Diablo III, Blizzard Entertainment, USA, 2011
Diablo, Blizzard North, USA, 1996
Duke Nukem 3D, 3D Realms, USA, 1996
Eye of The Beholder II: The Legend of Darkmoon, Westwood Associates, USA, 1991
Fallout, Interplay Entertainment, USA, 1997
Minecraft, Mojang, Swedish, 2009
MUD1, Roy Trubshaw & Richard Bartle, UK, 1978
Pac-Man, Namco, Japan, 1980
Populous, Bullfrog, UK, 1989
StarCraft II, Blizzard Entertainment, USA, 2010
Sub-Roc 3D, Sega, Japan, 1982
Zaxxon, Sega, Japan, 1982
Images
Cover Image (Tesseract). Created by A. Petrovits and A. Canossa
Image 1 (The Penrose Triangle). Created by A. Petrovits and A. Canossa
Image 2 (Regular Polyhedra). Created by A. Petrovits and A. Canossa
Image 3A and 3B (Penrose Triangle Possible 3D Modeling Variations). Retrieved from http://www.cs.technion.ac.il/~gershon/EscherForReal/
Image 3C and 3D (Penrose Triangle Possible 3D Modeling Variations). Created by A. Petrovits and A. Canossa

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
